Here is a formula for
a centrifugal pump that clearly? Shows that Tracy and Lynn are
correct
Energy Usage
The energy usage in a pumping installation is determined by the flow
required, the height lifted and the length and characteristics of the
pipeline. The power required to drive a pump (Pi), is defined
simply using SI units by: by:
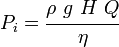
where:
Pi is the input
power required (W)
ñ is the fluid density
(kg/m3)
g is the gravitational constant
(9.81 m/s2)
H is the energy Head added to
the flow (m)
Q is the flow rate
(m3/s)
ç is the efficiency of the pump
plant as a decimal
One can see that if Q
the flow rate becomes zero (by blocking the exit) then the power required to
drive the pump Pi also becomes zero. So block the pump and lower the
flow and the power required drops – or with the same power, the pump can spin
faster. There is always some flow around the vanes of a centrifugal pump
in reality, so the power does not cause the pump to spin to infinity rpm but
it equalizes at a higher rpm than when considerable (unblocked) flow is the
condition.
Is this fun or
what?
From:
Rotary motors in aircraft
[mailto:flyrotary@lancaironline.net] On
Behalf Of Lynn Hanover
Sent: Tuesday, August 18, 2009 2:55
PM
To: Rotary motors in aircraft
Subject: [FlyRotary] Swirl pots/box
fans
NO! I meant exactly
what I wrote. It is admittedly counter-intuitive but true none the
less. Did you attempt to prove it to yourself with the suggested
test? Only takes a few seconds :>)
Tracy
On Tue, Aug 18, 2009 at 11:57 AM, Jeff Luckey <JLuckey@pacbell.net>
wrote:
When a box fan falls over onto its suction side, it
revs up as the work it is performing drops off to near
zero.....................same idea.